問1 温度モニタに関する次の記述を読んで，設問1～3に答えよ。

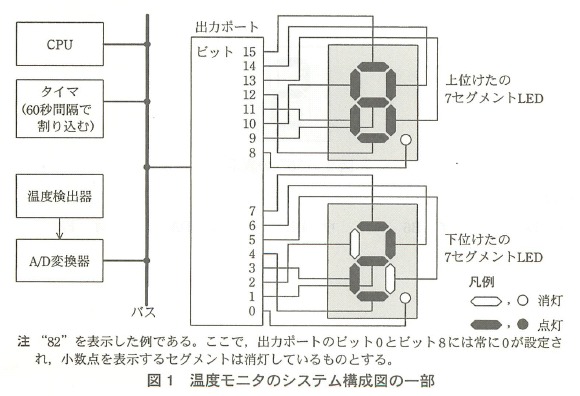
 図1に温度モニタのシステム構成図の一部を示す。

温度の検出範囲は0～99℃とし，対応するＡ／Ｄ変換器の出力値は，
0～99の16ビット符号なし2進数とする。

このシステムは，タイマ割込み発生時に起動される割込みプログラムの中で
温度検出器の出力地をＡ／Ｄ変換器を介して取り込み，
2個の7セグメントLEDには10進数の数字１けたを表示する。

検出された温度0～99℃に対して，表示器では"00"～"99"として表示する。

LEDの各セグメントは，対応する出力ポートのビットの値が1のとき点灯し，0のとき消灯する。
7セグメントLEDに，"0"～"9"の数字を表示するために，
対応する8ビットのデータを数字の字形に合わせて設定する。
これらを形状データという。

割込みプログラムが起動するＡ／Ｄ変換の開始から，
表示処理の完了までの時間は，タイマ割込み間隔に比べて充分短い。

各機器に割り当てられたI/Oポート番号を指定して行う。
7セグメントLEDが接続されている出力ポートには
I/Oポート番号1が，Ａ／Ｄ変換器にはI/Oポート番号2と3がそれぞれ割り当てられている。
表1に出力ポートとＡ／Ｄ変換器の動作概要を示す。




設問1
下位７けたの７セグメントLEDに図2のように"5"を表示したい。
出力ポートのビット7～0に設定すべき形状データとして正しい答えを，解答群の中から選べ。
ここで，形状データはビット7を最上位ビットとする16進数で表記する。



解答群
ア 66     イ B6     ウ BE     エ DA     オ F2

＜解説？＞
図１をよく見てください。
下位桁の0～7がそれぞれ対応する部位を黒く染めていると考えるとわかりやすいかと思います。
そして設問の１、"５"を表示するには、
下記解説図を参照してください。



上記のように5を表示するための対応部位がそれぞれ0～7の値となります。
この図の値をもう少しわかりやすくすると、

7	6	5	4	3	2	1	0
1	0	1	1	0	1	1	0

上位4桁

8	4	2	1
1	0	1	1

(8+2+1)=11
16進数なので値は"B"

下位4桁

8	4	2	1
0	1	1	0

(4+2)=6
値は"6"

値を並べて”B6”

答えはイ


設問2
タイマ割込み発生時に起動される割込みプログラムについて，その処理の流れを図3に示す。
図3の処理中の【】に入れる正しい答えを，解答群の中から選べ。
なお，処理中で使用している擬似命令の意味は表2のとおりとする。





解答群
ア INPUT 1     イ INPUT 2     ウ OUTPUT 1     エ OUTPUT 2     オ OUTPUT 3

＜解説？＞
さて、この問題も特に難しいことはありません。
先ほど提示された資料、表の1をよく見てください。下記にて噛み砕いて説明します。

番号	概要
1	番号1に形状データを書き込むとLEDに値を出す(A)
2	2番に1を書き込むとＡ／Ｄ変換開始(B)
	2番から読み込んだ値が0なら変換中(C)
	2番から読み込んだ値が0以外なら変換完了(D)
3	変換完了後に番号3から読み込むとＡ／Ｄ変換後の値が出る(E)

要約すると上記の表のような解釈ができると思います。
問題の【a】，【b】は変換中かどうかのループの前の処理なので変換完了していないことがわかります。
ので、3の値が含まれているオは選択肢から外れます。

【a】について考えてみます。
Ａ／Ｄ変換開始なので上記表で当てはまるものは(B)と言えそうです。
(Ｂ)は要約するとI/Oポートの2番に1を書き込むということなので，
【a】の答えはエのOUTPUT1(1を書き込む)になります。

次は【b】について考えてみます。
先ほどと比べると処理概要が記載されていない分情報は少ないですが，前処理，後続処理で考えてみます。
前処理は[Ａ／Ｄ変換開始]後続処理は[GRの中が0なら処理中]となります。
この時最初に設定したGR=1の値が変化している事に着目します。
つまり、GRの中身に影響を与える処理を【b】はしている事になります。
表の2を読むとGRに影響する操作はINPUT処理だけなのでこの時点で選択肢はア・イのどちらかになります。
上記表より読み込むポート先は2しかありえないので
【b】の答えはイのINPUT2(2のポートの情報をGRに書き込む)になります。

設問3
割込みプログラムの中で呼び出す手続DISPLAYの仕様と実行例は次のとおりである。
実行例に関する記述中の【】に入る正しい答えを，解答群の中から選べ。

[手続DISPLAYの仕様]
DISPLAYはGRに設定されたデータが示す値を表示器に表示する。

7セグメントLEDに"0"～"9"の数字を表示するために，
それぞれ8ビットからなる10個の形状データを表としてプログラム中に保持している。

GRに設定されたデータは，検出した温度に対応する0～99の16ビット符号なし2進数であり，
このまま出力ポートに設定しても意図した表示にはならない。

GRの内容を図4のとおり2桁のBCD(2進化10進数)に変換し，表を引き，
各けたに対応した形状データを図5のとおりにGRに設定して出力ポートに書き込む。



[手続DISPLAYの実行例]
図5のGRの内容が16進数表記でFEFCであったとき，
BCD値を格納していた図4のGRの内容は16進数表記で【c】であり，
割込みプログラムから手続DISPLAYに渡されたGRの内容は16進数表記で【d】である。

＜解説？＞
後ほど解説を入れます

cに関する解答群
ア 0008     イ 0309     ウ 0800     エ 0903     オ 0907

dに関する解答群
ア 0008     イ 0027     ウ 0050     エ 005D     オ 0061

QC(QualityControl)七つ道具

QCについては初級システムアドミニストレータの試験でもでているので復習がてら、、

QCとは品質的管理手法のことで、
品質を維持、原因の特定などの管理のための数値的データのこと。

①パレート図
値が降順にプロット（描画、点を打つなどの意)された棒グラフ、折れ線グラフのこと。
目的は要因の中からもっとも重要なものを浮き彫りにすることにある。

②ヒストグラム(柱状グラフ)
縦軸に度数、横軸に階級をとった統計グラフの一種。
目的はデータの分布状況を視覚的に認識することにある。

③チェック・シート
データの取得、整理を容易にし点検、確認項目が漏れなく行えるように
あらかじめ設計された様式。フォーマット。

④管理図
時間ごとの状態をグラフ上に配置し、
従来までの傾向と異なるデータや管理限界線を逸脱したデータの有無で
品質、製造工程が安定な状況で管理されているかを判断する。

⑤特性要因図
特性と要因の関係を系統的に線で結んで（魚の骨の様な形になることからフィッシュボーンとも呼ばれる）
表した図。目的は大抵、原因を追究することにある。
特性とは、管理の成績、成果として得るべき指標（不良率や在庫金額など、）
要因とは、特性に影響する管理事項のこと。
原因とは、多くの場合適切な管理を欠いた故にトラブルを引き起こした要因のこと。

⑥グラフ
複数の統計データの整理、視覚化、分析などに用いられるもの。

⑦散布図
縦軸、横軸に2項目の量や大きさなどを対応させ、データを点でプロットしたもの。
目的は2項目の相関を調べることにある。
右上がりだと正の相関、右下がりだと負の相関が2項目間にあると言える。

以上がQC七つ道具とされている。
wikiや手持ちの資料などを参考にして自分なりにまとめた為勘違いなどがあるかもしれません。

しかし、他のツールは別として、「グラフ」というのは少し大別過ぎる気がするんですがね。
そういう意味での大別だとグラフのなかにヒストグラムも含まれる気がしてならないのですが。

恐らく何か決定的な違いがあるのでしょうが、偉い人の考えることはわかりませんねぇ。

文字に起こすと何かとても難しいように感じますが単語、文章を区切って考えればそんなに難しいことは無いはずです。

QC七つ道具は初級システムアドミニストレータを始めとして、色々な企業で使われている手法です。
（もちろん各々改良を加え最適化して使っているとは思いますが）

それでは今回はこれで。

さて月曜日までの連休ですので、がんばって勉強を始めます。
今回は数値の表現方法です。
・数値の表現
・コンピュータの内部では限られたビットで数値や文字などを表現しなくてはいけません。
・それでは限られたビット数での表現の仕方を勉強しましょう。
2進数の場合での表現から見ていきます。
①絶対値表現
最上位のビットで符号を表示する方法です。正の数の場合は、最上位の桁を0。
負の数の場合は最上位桁を1とします。
3という数字を2進数で8ビットで表すと00000011です、
-3は10000011です。赤文字で示したところが符号になっているわけです。
ただし、この表現では0の表現として00000000と10000000と二つ存在することになります。
②補数表現
もっとも良く使われるのはこちらの表現で、
基数から表現しようとする数を引き算したものです。
1の補数を表現するには2進数のすべてのビットを反転させます。
たとえば-3を表現したいとします。すると
3の表現である00000011を反転させて、11111100を-3とします。
8ビットの場合127～-127を表すことが出来ます。
ただし、0の表現に00000000と11111111との二通りが存在することになります。
次は2の補数です。
2の補数は先ほどと同じように2進数のすべてのビットを反転させて1を足します。
-3を表現したい場合は3の表現00000011を反転し11111100にして、
1を足すと、11111101これを-3とします。
2の補数の場合は0の表現は00000000のみとなります。このため、
絶対値表現、1の補数に比較すると表すことの出来る数の範囲が1つ増えます。
8ビットの場合は127～-128を表すことが出来るのです。

小テスト)
問１)8ビット・1の補数表現で表すことの出来る範囲はいくつですか。
127～-127
問２）8ビット・2の補数表現で表すことの出来る範囲はいくつですか。
127～-128

ちょっと集中が続かないので今回は短めですがこれでおしまいですｗ
次回は浮動少数点数についてまなびます。

・2進数から8進数、16進数への変換
もうこの時点で萎えそうなのはもう書き終えるころに
間違えてすべてを消してしまったからに他なりません、、俺の馬鹿・・
・8進数への変換方法は3ビットずつ区切って変換します。
はい、2度目ですから。
ちなみに変換方法は2進数から10進数にするのと基本は変わりません。
・16進数への変換方法は4ビットずつ区切って変換します。
3ビットとか4ビットとか訳分からなくなりがちですが
それぞれ3桁4桁と読み替えてください。
例題）1101.101を8進数、16進数への変換
まずは8進数から。
3桁ずつだから、
1｜101｜.101　ですね。
次は変換です。先頭の１から。
2の1乗=1なので1
次の101は
2の1乗=1
2の2乗=2しかし0なので存在しない
2の3乗=4
1+0+4=5なので5
次の.101は変換した結果は先ほどと同じなので5
しかし小数部なので答えは0.5
答えは15.5
次は16進数への変換
4桁で区切るので
1101｜.101
1101から先に変換してしまいます。
2の1乗=1
2の2乗=2しかし存在しないので0
2の3乗=4
2の4乗=8
1+0+4+8=13
しかし16乗なので
1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
のいずれかで示されるので
13=16進数ではD
次は.101ですが、4桁区切りであるので.1010と示されます。
それでは変換。
2の1乗=1しかし存在しないので0
2の2乗=2
2の3乗=4しかし存在しないので0
2の4乗=8
0+2+0+8=10
10=16進数ではA
しかし小数部なので.A
16進数の答えはD.Aです。
なんだかアルファベットが入ると数字じゃないみたいだねぇ。
でも間違いなく16進数です。
さて次。
問1)2進数の10011は8進数でいくつか。
10｜011
このあたりから計算方法をすこし割愛していきます。
それでは10から
10=2
次は011
011＝3
答えは23
問2)16進数のF2は2進数でいくつか。
解き方は一桁ずつ区切って考えていくことが肝です。
まずはFから、10進数で言うとFは15のことです。
16進数は4ビット（桁）ずつ区切って変換したことを思い出してください。
ここからは計算能力のない私独自のワールドです。
16進数のFつまり15にするには2の1乗から2の4乗の間で、
どれを足せば実現できるかで考えます。
0と1のスイッチがあると考えてください。
足す数字は1足さない数字は0として
この場合15は
2の1乗=1　1
2の2乗=2　1
2の3乗=4　1
2の4乗=8　1
1+2+4+8=15とすべて足すと15になるので
1111になる。
次は2
2の1乗=1　0
2の2乗=2　1
2の3乗=4　0
2の4乗=8　0
この場合は2の2乗で事足りるので、
したから並べて0010になる。
これを順番に並べて
答えは11110010

さてこれでn進数への変換はひと段落つきましたが、
これからもしばらく進数や数値の表現の方法を学んでいきます。
眠くなるようなことが続きますががんばっていきましょう。
次回は補数を含めた浮動小数点数について学びたいと思います。
チラッと見た感じだと非常に難しいです。

・「コンピュータの内部は0か1のどちらかで表現されます。」
２進数ですね。これについては分かります。
・「0、1で表せる情報量を1ビットといいます。」
・「2ビットでは、(00,01,10,11)と4種類表せます、つまり2の2乗です。」
う、うむ…ｗ
・「８ビットあると2の8乗つまり256種類を表せます。」
この辺は初級シスアドでもしたな。8ビットは1バイトなんだよな。
この辺は少し割愛します。
・「n進数から10進数への変換。」
ここからが数学的なんだよな、、算数ですでに諦めた俺の計算能力が唸りを上げるぜ。
例題)101を10進数に変換
一桁目が１なので2の1乗＝1
二桁目が0なので2の2乗＝2しかし0なので存在しません。
三桁目が1なので2の3乗＝4
というわけで1+0+4=5
答えは5！
なんだかんだで正解。
・「少数部の変換」
げ。
例題)1011.01
まずは整数部から先ほどの要領で、、
一桁目は＝１
二桁目は＝２
三桁目は０なのでスルー
四桁目は＝８
足し算1+2+0+8=11と。
小数部は左から順に解きます。
.01なので、
2の-1乗、、とは！
解説を読みますｗ
2分の１のことらしい。つまり、、0.5か？しかし0なので存在しない。
次は2の-2乗＝4分の１＝0.25か？
多分-のべき乗は（2ｘｎ乗）分の1らしい？
てことは答えは0.25か。
整数部と足しこんで11.25！
ふうｗさて、次。
・「10進数からｎ進数への変換」
まぁやっぱこうくるわな。
・「10進数をnで割ったあまりを求める」
う～ん？ｗ
例題）６を2進数に変換
2)6--0
2)3--1
2)1

赤で示したのが割ったあまりです。
この余りをしたから順に並べます。
110
これが6を2進数で表した数字です。次！
・「小数部の変換」
・「小数部をnで掛けて整数部を求める。」
結構言葉で表すとなると分かりにくいですね。というわけで例題
例題）0.25を2進数に変換
0.25ｘ2＝0.5
0.5ｘ2＝1
赤で示したのが整数部なので
.01
つまり0.01です。
では次は応用！
例題）10進数61.125を2進数に変換
整数部から
2)61
2)30--1
2)15--0
2)7--1
2)3--1
2)1--1
111101
次は小数部
0.125x2=0.25
0.25x2=0.5
0.5x2=1
0.001
答えは111101.001
コツはつかめたかな。

・小テスト
問１)2進数の100は10進数で表すといくつか。
2の1乗=1 しかし存在しない
2の2乗=2 しかし存在しない
2の3乗=4
存在するのは4のみなので答えは4

問2)10進数の8は2進数ではいくつか。
2)8
2)4--0
2)2--0
2)1--0
答えは1000

問3)10進数の0.75は2進数ではいくつか
0.75x2=1.5
1.5x2=3.0
とここまで解いたところであれ？となってしまった。
2進数に直すのだから3なんて数字出てきてはいけないはず。
少しぐぐってみたらすぐに分かった。
どうやら掛けた結果に整数部がでてきたら整数部は切るらしい。
つまり、
0.75x2=1.5 //しかし小数部だけをとりだす。
0.5x2=1.0
答えは0.11というわけだ。

今回は2進数メインで進めたが次は他の進数にも直していきます。
次回は10進数から8進数16進数への変換です。